Aprender Geometría puede ser muy divertido!!: 11/01/12

RePaSaMoS ;)

Actividades de repaso y refuerzo

Recuerda:

•Según sus lados, los triángulos se clasifican en:

ØEquiláteros à si tienen tres lados iguales.

ØIsóscelesà si tienen dos lados iguales.

ØEscaleno à si tienen tres lados desiguales.

• Según sus ángulos, los triángulos se clasifican en:

Ø Rectángulos à si tienen un ángulo recto.

ØAcutángulos à si tienen tres ángulos agudos.

ØObtusángulos à si tienen un ángulo obtuso.

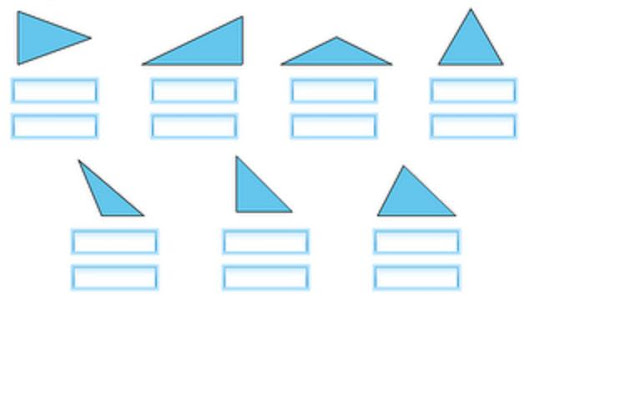
Completa las fichas:

Número de lados iguales :
Número de ángulos agudos :
Número de ángulos rectos à
Número de ángulos obtusos à
Según sus lados,es un triángulo à
Según sus ángulos, es un triángulo à

Número de lados iguales :
Número de ángulos agudos :
Número de ángulos rectos à
Número de ángulos obtusos à
Según sus lados,es un triángulo à
Según sus ángulos, es un triángulo à

Número de lados iguales :
Número de ángulos agudos :
Número de ángulos rectos à
Número de ángulos obtusos à
Según sus lados,es un triángulo à
Según sus ángulos, es un triángulo à

Recuerda:

•Los cuadriláteros se clasifican, según sus lados en:

ØTrapexoides si no tienen lados paralelos.

ØTrapecios si tienen dos lados paralelos.

ØParalelogramos si tienen los lados paralelos dos a dos.

• Los paralelogramos se clasifican , según sus lados y sus ángulos en:

ØCuadrados si tienen cuatro lados iguales y cuatro ángulos rectos.

ØRectángulos si tienen lados iguales dos a dos y cuatro ángulos rectos.

ØRombo si tienen cuatro lados iguales y los ángulos iguales dos a dos.

ØRomboides si los lados y los ángulos son iguales dos a dos.

Relaciona cada figura con su nombre:

Trapezoide Trapecio Cuadrado Rectángulo Rombo Romboide

Recuerda:

üDos figuras son simétricas respecto a un eje si al doblar por ese eje las dos figuras coinciden.

üAl mover una figura en la cuadrícula, hacemos una traslación.

Traza la figura geométrica respecto al eje de simetría:

Recuerda:

Según el número de lados, los polígonos pueden ser:

triángulos, si tienen tres lados; cuadriláteros, si tienen cuatro lados;

pentágonos, si tienen cinco lados; hexágonos, si tienen seis lados;

heptágonos, si tienen siete lados; octógonos, si tienen ocho lados;

eneágonos, si tienen nueve lados; decágonos, si tienen diez lados.

Observa el polígono y contesta:

•¿Cuántos vértices tiene este polígono?

•¿Cuántos lados tiene este polígono?

•¿Cuál es su nombre?

Ahora, repasa de rojo los lados del polígono y marca en azul los ángulos

CÁLCULO MENTAL

CÁLCULO MENTAL

- Calcula la diferencia entre:

45 y 53

23 y 31

56 y 62

37 y 42

74 y 81

65 y 72

- Cuenta de 15 en 15 desde 15 hasta 255; de 20 en 20 desde 7 hasta 307; de 25 en 25 desde 25 hasta 600.

- Suma:

7,5 + 1,5= 8,5 + 2,5= 32,5 + 3,5=

2,5 + 6,5= 2,5 + 4,5= 20,5 + 5,5=

12,5 + 4,5= 64,5 + 0,7= 8,9 + 3,9=

- Resta:

5,5 - 2,5= 8,5 - 1,5= 8,5 - 1,5=

15,5 - 1,5= 26,5 - 3,5= 6,5 - 1,5=

16,5 - 5,5= 20,5 - 3,5= 53,8 - 1,8=

- Divide mentalmente:
80:10= 1.500:100= 19.400:100=
72.000 : 1.000= 1.000:1.000= 4.00:100=

MULTIPLICAR POR 0,1 es igual

que dividir entre 10.

28 · 0,1 = 2,8

ACTIVIDADES:

Multiplicar y dividir por 0,1:

8 x 0,1 =	18 x 0,1 =	85 x 0,1 =
24 x 0,1 =	4 x 0,1 =	94 x 0,1 =
50 x 0,1 =	5 x 0,1 =	51 x 0,1 =
100 x 0,1 =	10 x 0,1 =	1000 x 0,1 =
7 : 0,1 =	78 : 0,1 =	75 : 0,1 =
37 : 0,1 =	379 : 0,1 =	87 : 0,1 =
73 : 0,1 =	13 : 0,1 =	63 : 0,1 =
100 : 0,1 =	1000 : 0,1 =	190 : 0,1 =

VAMOS CHICOS!!!JUGUEMOS UN RATO...

Multiplicamos y dividimos por 10, 100 y 1000

http://www.google.com/url?q=http%3A%2F%2Fwww.genmagic.net%2Fmates4%2Fser8c.swf&sa=D&sntz=1&usg=AFrqEzc9LqtaABkcDPZSnteaFYcOiyYUDw

Multiplicamos decimales

http://ntic.educacion.es/w3/eos/MaterialesEducativos/mem2008/visualizador_decimales/multiplicaciondecimales.htm

Multiplicación por la unidad seguida de ceros

http://www2.gobiernodecanarias.org/educacion/17/WebC/eltanque/todo_mate/mult_deci/mult_deci_p.html

La división(cálculo mental)

http://ntic.educacion.es/w3/recursos/primaria/matematicas/decimales/menuu7.html

Practico la división por la unidad seguida de ceros

http://www2.gobiernodecanarias.org/educacion/17/WebC/eltanque/todo_mate/usc/divideci/divi_usc_ed_p.html

LA CIRCUNFERENCIA Y EL CÍRCULO

CIRCUNFERENCIA Y CÍRCULO

Una circunferencia es una línea curva, cerrada y plana cuyos puntos están a la misma distancia de

otro punto llamado centro.

Un círculo es la figura plana limitada por una circunferencia.

Los elementos de la circunferencia y del círculo son: diámetro, radio, cuerda y arco.

LONGITUD DE LA CIRCUNFERENCIA

La longitud de una circunferencia es un poco mayor que el triple de su diámetro. Para calcularla, hay que multiplicar el diámetro por 3,14 (llamado Pi).

Por ejemplo, la longitud de una circunferencia de 5 cm de

diámetro es: L = 5 x 3,14 = 15, 7 cm.

ACTIVIDADES:

Dibuja en tu cuaderno una circunferencia como esta y señala en ella:

a) Un diámetro

b) Una cuerda

c) Un arco

Copia la tabla y calcula la longitud de una circunferencia cuyo diámetro mida:

DIÁMETRO	LONGITUD DE LA CIRCUNFERENCIA
7cm
9cm
11cm
13cm

¿Cuál será la longitud de la cuerda una vez estirada?

Traza un círculo de 2cm de radio y señala sobre él dos diámetros. ¿Qué nombre recibe cada una de las cuatro zonas en las que ha quedado dividido el círculo?

Copia esta figura y coloca en ella:

a) Un segmento circular

b) Dos sectores circulares iguales

c) Un semicírculo

Observa el dibujo y calcula la distancia que recorrerá el burro después de dar 20 vueltas.

ACTIVIDADES INTERACTIVAS DE LA CIRCUNFERNECIA Y EL CÍRCULO

Aquí tenéis una serie de actividades que tienen una explicación por si os queda alguna duda....así repasaréis lo que hemos dado!!

http://www.eskola20.org/sd/6to/mat/circunferencia_circulo/modulos/es/content_1_1.html

http://www.ceipjuanherreraalcausa.es/Recursosdidacticos/QUINTO/datos/03_Mates/datos/05_rdi/ud12/7/07.htm

http://www.genmagic.org/mates2/cir1c.swf

Los CUADRILÁTEROS

Un cuadrilátero es un polígono que tiene 4 lados. Al ser un polígono, dos lados contiguos no pueden estar alineados.

Los cuadriláteros tienen distintas formas pero todos ellos tienen cuatro vértices y dos diagonales. En todos los cuadriláteros la suma de sus ángulos interiores es 360º.

Sus elementos característicos son: lados, vértices, ángulos y diagonales.

Clasificación de los cuadriláteros:

Los cuadriláteros se pueden clasificar según el paralelismo entre sus lados en:

Trapezoides--> Los lados no son paralelos

Trapecios--> Dos lados paralelos

Paralelogramos--> Lados paralelos dos a dos

A los cuadriláteros que tienen los lados paralelos dos a dos, es decir, sus lados son siempre opuestos, se les llama paralelogramos. Son paralelogramos, por tanto, el cuadrado, el rectángulo, el rombo y el romboide:

Cuadrado es el paralelogramo que tiene sus cuatro ángulos y sus cuatro lados congruentes. Recordamos lo que significa CONGRUENTES? Congruentes quiere decir que sus cuatro ángulos, al igual que sus cuatro lados, son iguales.

Rectángulo es el paralelogramo que tiene sus cuatro ángulos rectos y sus diagonales son congruentes.

Rombo es el paralelogramo que tiene sus cuatro lados congruentes y sus diagonales son perpendiculares.

Romboide es el paralelogramo que tiene dos pares de lados paralelos e iguales entre sí formando dos pares de ángulos también iguales entre sí; lados y ángulos iguales dos a dos.

Ahora que sabemos todos estos conceptos, os

proponemos un juego!!

Adivina adivinanza...Adivina, adivinanza..!!

Actividades:

Esta actividad será para hacer en lápiz y papel de manera individual para entregar.

Verdadero o Falso ¿? Actividad para realizar en pequeños grupos rodeando con un círculo la respuesta elegida por tod@s.

El cuadrado, el rombo y el rectángulo son paralelogramos. V / F
Los rombos tienen todos los lados iguales, por tanto el cuadrado es un rombo. V / F
Los paralelogramos tienen sus lados opuestos iguales y contenidos en rectas paralelas. V / F
El trapecio es un paralelogramo. V / F
El rectángulo tiene sus cuatro ángulos rectos, por tanto el cuadrado es rectángulo. V / F
El cuadrado es rectángulo y rombo a la vez. V / F

Actividad individual de lápiz y papel:

¿Podrías justificar por qué la suma de los ángulos

interiores de un cuadrilátero suman 360º?

Para ayudaros, os sugerimos que dibujeis un cuadrilátero y tracéis una diagonal. Esta divide al cuadrilátero en dos triángulos, verdad? Pues acordaros de la suma de los ángulos interiores de un triángulo.. verás que fácil es!!

Sumamos los ángulos de los triángulos, es posible?

La suma de los ángulos interiores de un triángulo es siempre igual a 180º . Observad:

Calcula los grados que miden los ángulos C, B , A en los siguientes triángulos teniendo en cuenta que los ángulos de un triángulo miden en total 180º

Dibuja los siguientes elementos:

Un octógono Un semicírculo Un romboide

Un rectángulo Un trapecio Un pentágono

Completa:

Los triángulos según sus lados pueden ser: ___________________,

___________________ y ___________________.

Los triángulos según sus ángulos se clasifican en: ________________,

______________________ y ______________________.

Los cuadriláteros se clasifican en: ___________________________, __________________ y ____________________.

Los paralelogramos son: el ______________, el ________________,

el __________________ y el __________________

Rompecabezas divertidísimo: El TANGRAM ;)

JUGUEMOS!!! :D

Elementos de un TRIÁNGULO...

Como hemos visto, un TRIÁNGULO, está compuesto de tres lados y tres

ángulos pero, qué más ELEMENTOS componen un triángulo?

VÉRTICES :

Son los puntos de origen de los segmentos y los nombramos con letras mayúsculas: A, B, C,.. Y, Z.

LADOS :

Son los segmentos de la poligonal y las designamos por las letras de sus extremos, en este caso AB, AC, BC, CA...

ÁNGULOS INTERIORES:

Son aquellos formados por cada par de lados consecutivos del triángulo. Se denominan por las tres letras mayúsculas de los vértices o por una letra griega ubicada entre los lados del ángulo.

Existen tres tipos de triángulos que diferenciamos según las medidas sus lados:

Triángulo EQUILÁTERO :

Como podemos observar, es aquél que tiene sus 3 lados iguales, es decir, de la misma longitud

y sus ángulos??!! Qué característica vemos que tienen?

Triángulo ISÓSCELES:

Mediante este dibujo, comprobamos como la característica de este triángulo es que tiene solo dos lados de la misma longitud
Por lo tanto, solo dos de sus ángulos miden también lo mismo.

Triángulo ESCALENO:

En el triángulo ESCALENO, podemos observar como sus tres lados que lo componen tienen longitudes distintas. Por lo tanto, sus ángulos también miden diferente.

Además de por sus lados, los triángulos se clasifican también según la medida de sus ángulos. Así tenemos otras tres divisiones:

Triángulo ACUTÁNGULO:

Es el que tiene todos sus ángulos agudos. Recordad que un ángulo agudo es aquél que mide menos de 90º, es decir, es más pequeño que un ángulo recto.

Triángulo RECTÁNGULO:

Es aquél que tiene un ángulo recto. Recordad que un ángulo recto es el que mide 90º y está formado por dos rectas perpendiculares

Triángulo OBTUSÁNGULO:

Es aquél que tiene un ángulo obtuso. El ángulo obtuso recordamos que es mayor que un ángulo recto y por tanto mide más de 90º.

Recordemos que los triángulos escaleno e isósceles pueden tener un ángulo recto. Un triángulo con un ángulo recto es el que tiene un ángulo de 90º. Es un triángulo denominado TRIÁNGULO RECTÁNGULO. El lado opuesto al ángulo recto se denomina HIPOTENUSA.